In version 3.2 of the TMS Analytics & Physics library, we’ve introduced new FNC Math components. The components allow easy development of math applications with all the advantages of the Delphi IDE. The base concepts of the math components have been described in the previous article. In this article, we’ll introduce several advanced components for designing more complicated math applications.

With the base components TFNCFunction1D, TFNCDerivative1D, and TFNCIntegral1D we can evaluate functions, derivatives, and integrals of math expressions. Let’s consider the following component:

• TFNCFunctionDerivative1D – introduces a symbolic derivative of an FNC function; allows evaluating the derivative for the specified variable value.

The component provides the following published properties:

• Variable (TVariableProperty) – a variable specifying the argument of the function.
• D (TVariableProperty) – a variable specifying the differential.
• Functional (TFNCBaseFunction1D) – a differentiable FNC function.
• Formula (TFormulaProperty) – read-only formula denoting the resulting math expression of the derivative.

As one can see, this component is like the TFNCDerivative1D, but the Functional property now is of TFNCBaseFunction1D type. This means that we can assign any appropriate function to the property. The component will trace the functional’s change and re-evaluate the derivative automatically.

Let’s start developing an advanced FNC math application. Put a TFNCProvider on the form and create three parameters ‘A’, ‘B’, and ‘L’. Add new TFNCFunction1D and TFNCFunctionDerivative1D components. Assign required properties to the function as described in this article. Add an FNC Chart and two plotters for both components (the function and the derivative).

Then connect the derivative component with the function, assigning its Functional property. Finally, input a simple math expression, say ‘5*sin(x)’, into the Formula property of the function. Our math application at the design time is shown in the picture below:

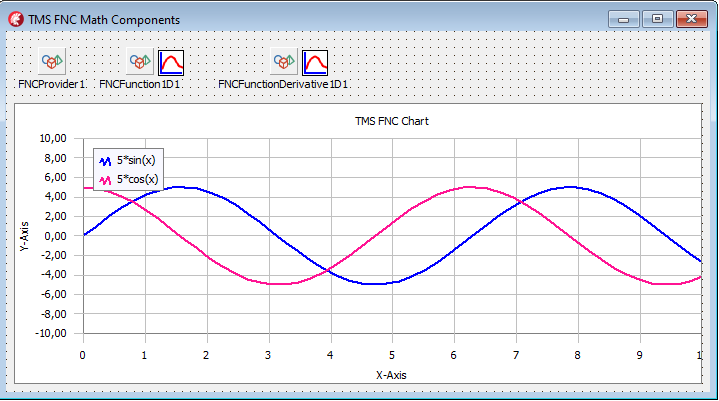
Then we can add a text box, allowing the user to input a math expression, and a button with the following simple event handler:

procedure
TForm1.Button1Click(Sender: TObject);
var
  f: string;
begin
  f:= Edit1.Text;
 
  FNCFunction1D1.Formula.Formula:= f;
end;

The developed application provides functionality for drawing a user-defined function and its derivative on one chart. An example of the running application is shown in the following picture:

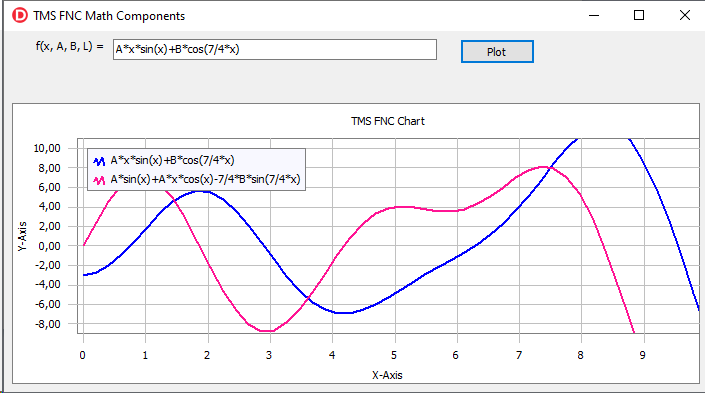
Note that we created only one button with the event handler which assigns the formula to the function. When the formula is changed, the derivative is re-evaluated and the chart is updated automatically.

Let’s move on and modify the application to evaluate also the second derivative of the function. It is possible due to the special structure of the FNC math components. As the TFNCFunctionDerivative1D class is a descendent of the TFNCBaseFunction1D, the derivative is considered to be an FNC function. Thus, we can just evaluate a derivative of any other derivative and get the second-order derivative of a function.

Putting a new TFNCFunctionDerivative1D component (together with a plotter for the FNC chart) and assigning the functional property to the first derivative component, we get the fully functional application:

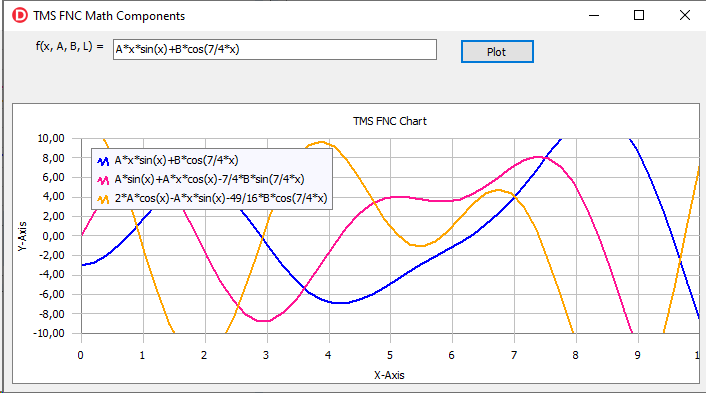
Finally, let’s consider the TFNCFunctionIntegral1D component. It has the same properties as the TFNCFunctionDerivative1D class, but it evaluates the indefinite integral of a function. Now we can create a single application that provides the evaluation of a user-defined function, its derivatives of the first and the second order, and its integral. 

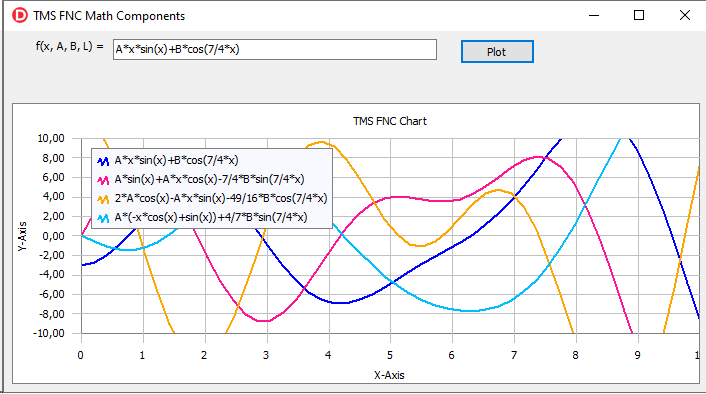
The source code of the demo project for the article can be downloaded from here. To develop your own FNC math application you need to install the TMS Analytics & Physics and TMC FNC Chart products.